Legendre 谱方法及其算例二

两点边值问题

考虑两点边值问题：

$$\left\{\begin{aligned} &-u''(y)+u(y)=f(y),\quad y\in \Lambda=(0,1), \\ &u(0)=1,\ u'(1)=0. \end{aligned} \right.$$

这里 ，通过变换方程的方式变到 的标准形式，再利用 Legendre 谱方法求解。

令 ，，，变换后的方程

$$\left\{\begin{aligned} &-4 U''(x)+U(x)=F(x),\quad x\in I=(-1,1), \\ &U(-1)=0, U'(1)=0. \end{aligned} \right.$$

其中 .

Legendre-Galerkin 方法

弱形式：

$$\left\{\begin{aligned} &\text{Find } U \in H^{1}(I) \text{ such that} \\ &4(U',v')+(U,v)=(f,v),\quad v \in H^{1}(I). \end{aligned} \right.$$

令 满足边界条件，可得

$$a_{k}=\frac{2k+3}{(k+2)^2},\quad b_{k}=-\frac{(k+1)^2}{(k+2)^2}.$$

记

逼近解展开

$$U_{N}(x)=\sum_{k=0}^{N-2} \hat{U}_{k} \phi_{k}(x) \in X_{N}.$$

谱格式：

$$\left\{\begin{aligned} &\text{Find } U_N \in X_N \text{ such that} \\ &4(U_N',\phi')+(U_N,\phi)=(f,\phi),\quad \phi \in X_N. \end{aligned}\right.$$

将 的展开式代入谱格式方程。令

$$\begin{aligned} &f_{k}=\int_{I} f_{N} \phi_{k} d x, \quad \boldsymbol{f}=\left(f_{0}, f_{1}, \ldots, f_{N-2}\right)^{T}, \\ &U_{N}=\sum_{j=0}^{N-2} \hat{U}_{j} \phi_{j}, \quad \boldsymbol{U}=\left(\hat{U}_{0}, \hat{U}_{1}, \ldots, \hat{U}_{N-2}\right)^{T}, \\ &s_{k j}=\int_{I} \phi_{j}^{\prime} \phi_{k}^{\prime} d x, \quad m_{k j}=\int_{I} \phi_{j} \phi_{k} d x, \\ \end{aligned}$$ $$S=\left(s_{k j}\right)_{0 \leq k, j \leq N-2}, \quad M=\left(m_{k j}\right)_{0 \leq k, j \leq N-2}.$$

取 ，可得到以下方程组

$$(4S+M) \boldsymbol{U}=\boldsymbol{f}.$$

刚度矩阵 是一个对角矩阵 [P146-4.22]，它的非零元素为

$$s_{kk}=-(4 k+6)b_{k}= \frac{(4k+6)(k+1)^2}{(k+2)^2}.$$

质量矩阵 是一个对称的五对角矩阵 [P146-4.23]，它的非零元素为

$$m_{jk}=m_{kj}=\left\{ \begin{aligned} &\frac{2}{2k+1}+\frac{2(2k+3)}{(k+2)^4}+\frac{2(k+1)^4}{(k+2)^4(2k+5)} , && j=k, \\ &\frac{2}{(k+2)^2}-\frac{2(k+1)^2}{(k+2)^2(k+3)^2}, && j=k+1, \\ &-\frac{2(k+1)^2}{(k+2)^2(2k+5)}, && j=k+2. \end{aligned}\right.$$

谱方法可以求解得到 ，通过变换 得到原方程的数值解。

数值求解

% LegenSM3.m
% Legendre spectral-Galerkin method for 1D elliptic problem
% -u_yy+u=f in [0,1] with boundary condition: u(0)=1, u'(1)=0;
% exact solution: u=(1-y)^2*exp(y);  RHS: f=(2-4*y)*exp(y);
% transformed equation: -4U_xx+U=F in [-1,1]
% boundary condition: U(-1)=0, U'(1)=0;
% exact solution: U=(1/2-1/2*x)^2*exp(1/2*x+1/2)-1;
% RHS: F=-2*x*exp(1/2*x+1/2)-1.
clear all; close all;
Nvec=3:18;
% Initialization error and condition number
L2_Err=[];  condnv=[];
% Loop for various modes N to calculate numerical errors
for N=Nvec
    [xv,wv]=legs(N+1);        % Legendre-Gauss points and weights
    Lm=lepolym(N,xv);         % matrix of Legendre polynomals
    yv=1/2*(xv+1);            % variable substitution 
    U=(1-yv).^2.*exp(yv)-1;   % exact solution
    F=(2-4*yv).*exp(yv)-1;    % RHS in [0,1] 
    
    % Calculting coefficient matrix
    e1=0:N-2;  e2=0:N-3;  e3=0:N-4;
    S=diag( (4*e1+6).*(e1+1).^2./(e1+2).^2 );     % stiff matrix
    M=diag(2./(2*e1+1)+2*(2*e1+3)./(e1+2).^4+2*((e1+1)./(e1+2)).^4./(2*e1+5))...
        +diag( 2./(e2+2).^2-2*(e2+1).^2./((e2+2).^2.*(e2+3).^2) , 1 )...
        +diag(2./(e2+2).^2-2*(e2+1).^2./((e2+2).^2.*(e2+3).^2),-1)...
        +diag( -2*(e3+1).^2./((2*e3+5).*(e3+2).^2) , 2 )...
        +diag(-2*(e3+1).^2./((2*e3+5).*(e3+2).^2),-2);  % mass matrix
    A=4*S+M;
    
    % Solving the linear system
    Pm=(Lm(1:end-2,:)+diag((2*e1+3)./(e1+2).^2)...
        *Lm(2:end-1,:)-diag((e1+1).^2./(e1+2).^2)*Lm(3:end,:));
    b=Pm*diag(wv)*F;       % solving RHS
    Uh=A\b;                % expansion coefficients of u_N(x)
    Un=Pm'*Uh;             % compositing the numerical solution
    
    L2_error=sqrt(((Un-U).^2)'*wv);  % L^2 error 
    L2_Err=[L2_Err;L2_error];
    condnv=[condnv,cond(A)];         % condition number
end
% Plot L^2 error
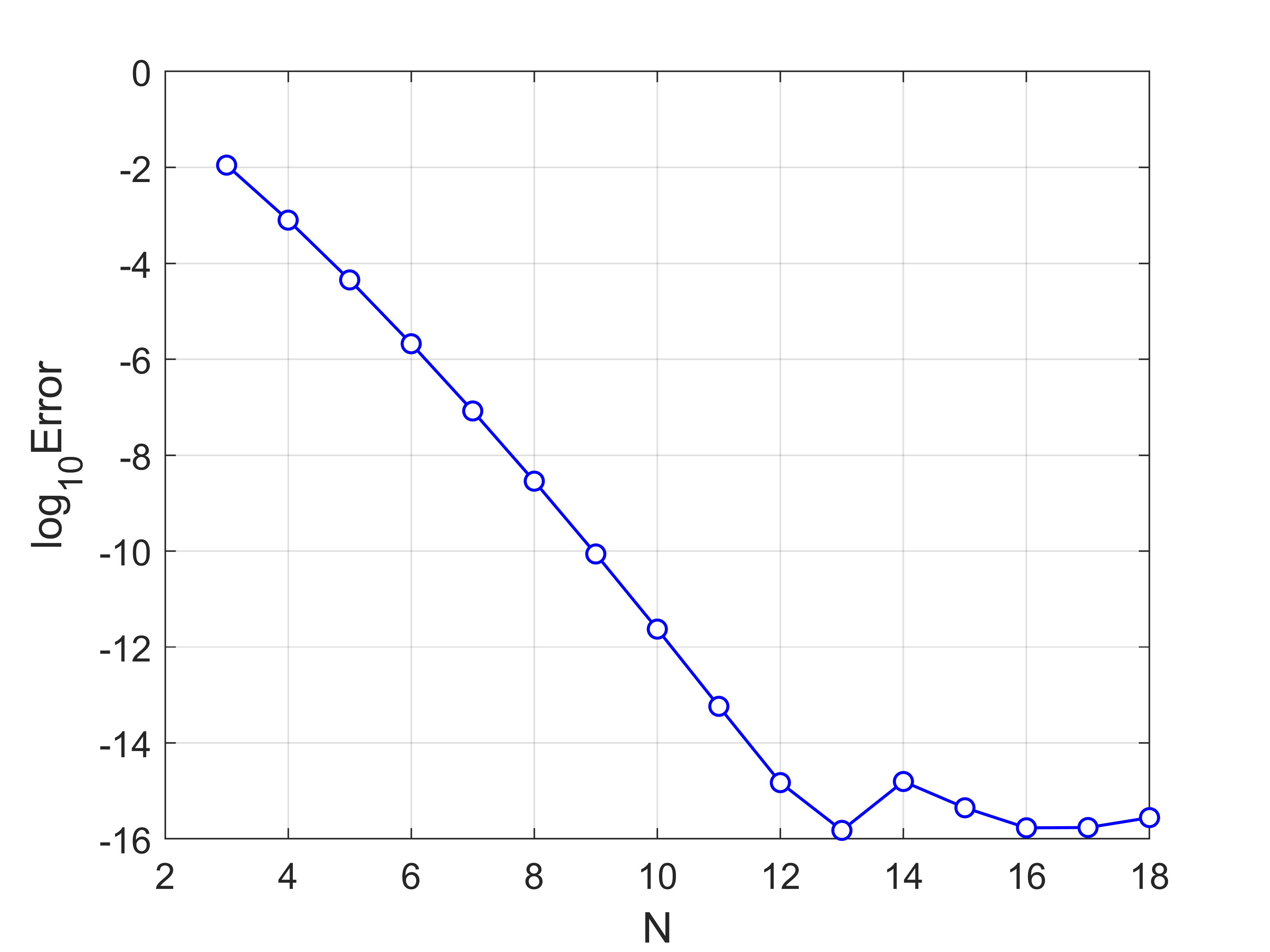
plot(Nvec,log10(L2_Err),'bo-','MarkerFaceColor','w','LineWidth',1)
grid on
%title('L^2 error of Legendre-Galerkin method','fontsize',12)
set(gca,'fontsize',12)
xlabel('N','fontsize', 14), ylabel('log_{10}Error','fontsize',14)

% sets axis tick and axis limits
xticks(2:2:18)
yticks(-16:2:0)
xlim([2 18])
ylim([-16 0])

% print -dpng -r600 LegenSM3.png
% print -depsc2 LegenSM3.eps

参考书籍

• Spectral Methods: Algorithms, Analysis and Applications.