一维热传导方程的 CN 格式

一维热传导方程 Crank-Nicolson 格式的 MATLAB 编程实现。

一维热传导方程

$$\left\{\begin{aligned} &\frac{\partial u}{\partial t}=a \frac{\partial^{2} u}{\partial x^{2}}+f(x, t), && 0<x<1,\ 0 <t \leqslant T,\\ & u(x, 0)=\phi(x), && 0 \leqslant x \leqslant 1, \\ & u(0, t)=\alpha(t), u(1, t)=\beta(t), && 0 < t \leqslant T. \end{aligned}\right.$$

其中 是正常数，、、 和 为已知函数。 为初始条件， 和 为边界条件。

Crank-Nicolson 格式

以空间步长 、时间步长 分别将 轴上区间 、 轴上区间 分成 、 等分，可得

$$x_{i}=j h, \quad 0 \leqslant j \leqslant M,$$ $$t_{n}=n \tau, \quad 0 \leqslant n \leqslant N.$$

一维热传导方程的六点对称格式（Crank- Nicolson格式）

$$\frac{u_{j}^{n+1}-u_{j}^{n}}{\tau}=\frac{a}{2}\left[\frac{u_{j+1}^{n+1}-2 u_{j}^{n+1}+u_{j-1}^{n+1}}{h^{2}}+\frac{u_{j+1}^{n}-2 u_{j}^{n}+u_{j-1}^{n}}{h^{2}}\right]+\frac{f(x_j,t_{n+1})+f(x_j,t_n)}{2},$$ $$u_{j}^{0}=\phi_{j}=\phi(x_{j}), \quad u_{0}^{n}=u_{M}^{n}=0.$$

以上格式可改写为

$$-\frac{r}{2} u_{j+1}^{n+1}+(1+r) u_{j}^{n+1}-\frac{r}{2} u_{j-1}^{n+1}=\frac{r}{2} u_{j+1}^{n}+(1-r) u_{j}^{n}+\frac{r}{2} u_{j-1}^{n}+\frac{\tau}{2}\left[f(x_j,t_{n+1})+f(x_j,t_n)\right].$$ $$1 \leqslant j \leqslant M-1,\ 0 \leqslant n \leqslant N-1.$$

即

$$-r u_{j+1}^{n+1}+(2+2r) u_{j}^{n+1}-r u_{j-1}^{n+1}=r u_{j+1}^{n}+(2-2r) u_{j}^{n}+r u_{j-1}^{n}+\tau f(x_j,t_{n+1})+ \tau f(x_j,t_n).$$ $$1 \leqslant j \leqslant M-1,\ 0 \leqslant n \leqslant N-1.$$

利用 和边值便可逐层求到 。六点对称格式是隐格式，由第 层计算第 层时，需解线性代数方程组（因系数矩阵严格对角占优，方程组可唯一求解）。

设

差分格式可以写为矩阵形式：

$$\boldsymbol{A} \boldsymbol{u}^{n+1}=\boldsymbol{B}\boldsymbol{u}^{n}+\boldsymbol{f}^n, \quad 0 \leqslant n \leqslant N-1.$$

其中矩阵 、、向量 的定义如下，注意向量 的首尾元素已包含了边界条件。

$$\boldsymbol{A}=\left(\begin{array}{ccccc}2+2 r & -r & & & \\ -r & 2+2 r & -r & & \\ & \ddots & \ddots & \ddots & \\ & & -r & 2+2 r & -r \\ & & & -r & 2+2 r \end{array}\right),$$ $$\boldsymbol{B}=\left(\begin{array}{ccccc} 2-2 r & r & & & \\ r & 2-2 r & r & & \\ & \ddots & \ddots & \ddots & \\ & & r & 2-2 r & r \\ & & & r & 2-2 r \end{array}\right),$$ $$\boldsymbol{f}^n= \left( \begin{array}{c} \tau f(x_{1},t_{n})+\tau f(x_{1},t_{n+1})+ru_0^{n}+ ru_0^{n+1} \\ \tau f(x_{2},t_{n})+\tau f(x_{2},t_{n+1}) \\ \vdots \\ \tau f(x_{M-2},t_{n})+\tau f(x_{M-2},t_{n+1}) \\ \tau f(x_{M-1},t_{n})+\tau f(x_{M-1},t_{n+1})+ru_M^{n}+ ru_M^{n+1} \\ \end{array} \right).$$

数值例子

$$\left\{\begin{aligned} &\frac{\partial u}{\partial t}=\frac{\partial^{2} u}{\partial x^{2}}+f(x,t), \quad 0<x<1, \quad 0 <t \leqslant 1, \\ &u(x, 0)=\sin (x), \quad 0 \leqslant x \leqslant 1, \\ &u(0, t)=\sin (t), \quad u(1, t)=\sin (1+t), \quad 0<t \leqslant 1. \end{aligned}\right.$$

其中 .

方程的真解：.

计算数值解

% fdm_cn.m
% Crank-Nicolson scheme for heat equation
% u_t=u_{xx}+f(x,t), (x,t) in (0,1)x(0,1],
% u(x,0)=sin(x), x in [0,1],
% u(0,t)=sin(t), u(1,t)=sin(1+t), t in (0,1].
% f(x,t)=cos(x+t)+sin(x+t),
% exact solution: u(x,t)=sin(x+t)
clear all; close all;
a=1;
h=0.05; x=[0:h:1];
tau=0.001; t=[0:tau:1];
r=a*tau/h^2;
M=length(x)-1; N=length(t)-1;
% constructing the coefficient matrix
e=r*ones(M-1,1);
A=spdiags([-e 2+2*e -e],[-1 0 1],M-1,M-1);
B=spdiags([e 2-2*e e],[-1 0 1],M-1,M-1);
% setting initial and boundary conditions
u=zeros(M+1,N+1);
u(:,1)=sin(x);
u(1,:)=sin(t); 
u(end,:)=sin(1+t);
for n=1:N
    F=tau*cos(x(2:M)'+t(n))+tau*sin(x(2:M)'+t(n))...
        +tau*cos(x(2:M)'+t(n+1))+tau*sin(x(2:M)'+t(n+1));
    F(1)=F(1)+r*u(1,n)+r*u(1,n+1);
    F(M-1)=F(M-1)+r*u(end,n)+r*u(end,n+1);
    % solving the system
    u(2:M,n+1)=A\B*u(2:M,n)+A\F;
end
% plot the figure
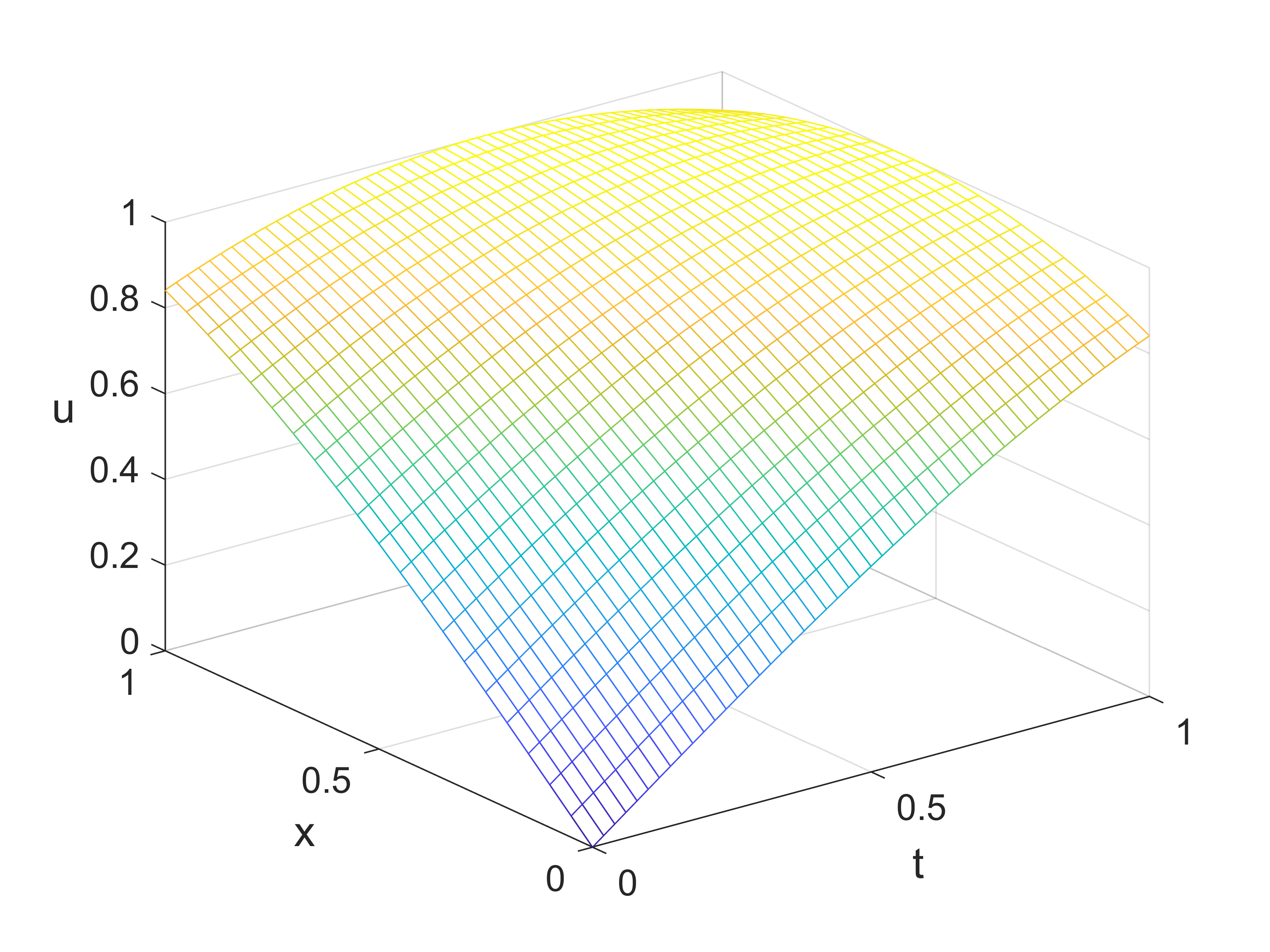
mesh(t(1:20:end),x,u(:,1:20:end))
set(gca,'fontsize',12)
xlabel('t','fontsize', 14) 
ylabel('x','fontsize',14)
zlabel('u','fontsize',14)

% calculating maximum error
[T X]=meshgrid(t,x);
ue=sin(X+T);

Error=max(max(abs(ue-u)))

% print -dpng -r600 fdm_cn.png
% print -depsc2 fdm_cn.eps

输出结果

Error =
   2.4988e-05