一维热传导方程差分方法的 MATLAB 编程实现。
一维热传导方程
其中
向前差分格式
以空间步长
一维热传导方程的向前差分格式
其中
以上格式可改写差分格式
先取
设
差分格式写成矩阵的形式:
其中矩阵
数值例子
方程的真解:
计算数值解
1 | % fdm_heat.m |
输出结果
1 | Error = |
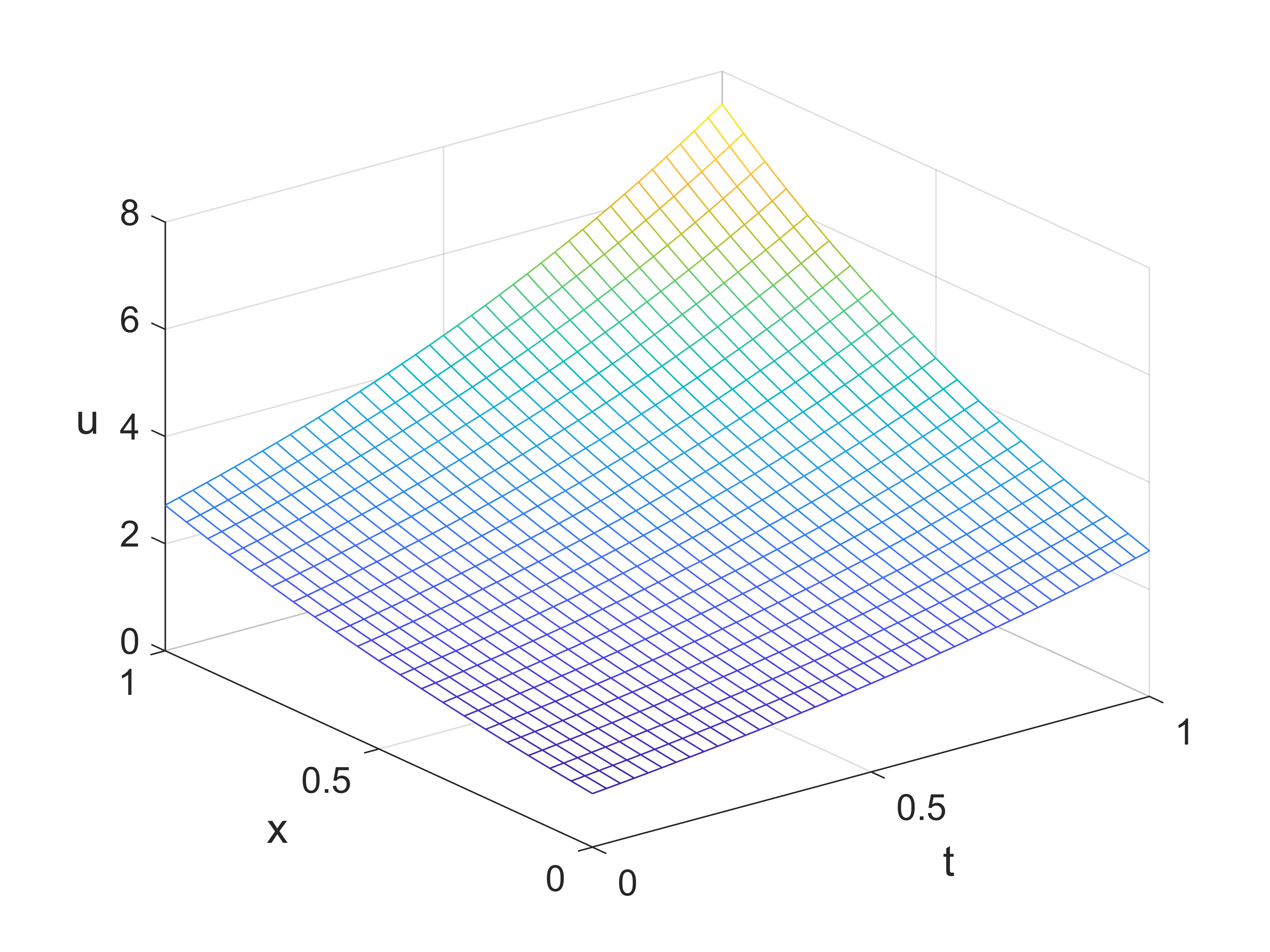
一维热传导方程差分方法的 MATLAB 编程实现。
其中
以空间步长
一维热传导方程的向前差分格式
其中
以上格式可改写差分格式
先取
设
差分格式写成矩阵的形式:
其中矩阵
方程的真解:
计算数值解
1 | % fdm_heat.m |
输出结果
1 | Error = |
