在偏微分方程的数值解法中,有限差分法数学概念直观,推导自然,是发展较早且比较成熟的数值方法。由于计算机只能存储有限个数据和做有限次运算,所以任何一种用计算机解题的方法,都必须把连续问题(微分方程的边值问題、初值问题等)离散化,最终化成有限形式的线性代数方程组。
学习有限差分方法,差分解的存在唯一性、收敛性及稳定性等理论知识请参考书籍《微分方程数值解法》(李荣华)。
这里重点介绍问题差分格式的 MATLAB 编程实现。
两点边值问题(常系数)
考虑二阶常微分方程边值问题(常系数):
其中
将区间
差分方程:
其中
以上差分方程对于
它的解
先定义向量
差分格式可以写为矩阵形式:
其中矩阵
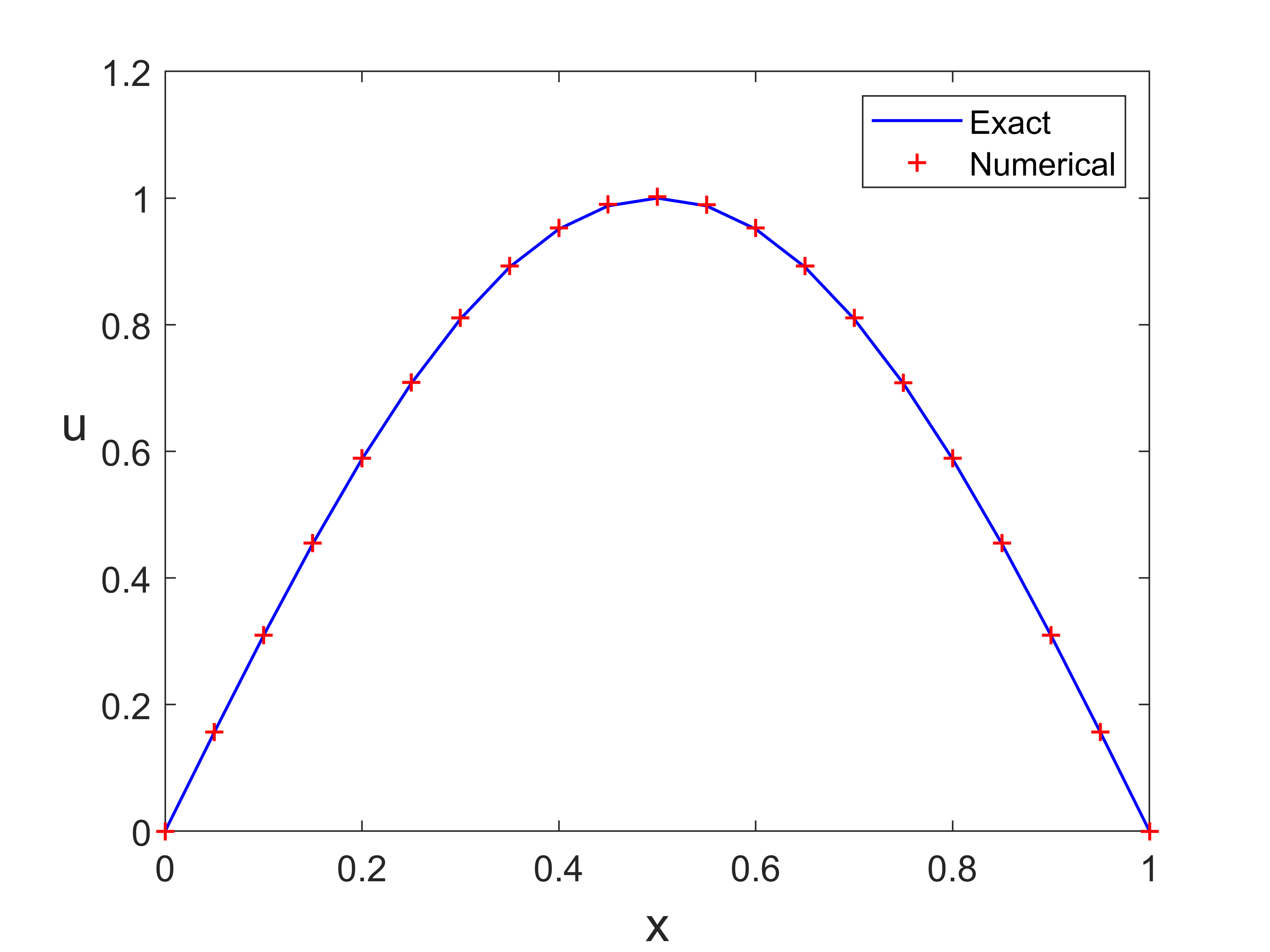
数值例子
方程的真解:
计算数值解
1 | % fdm1d1.m |
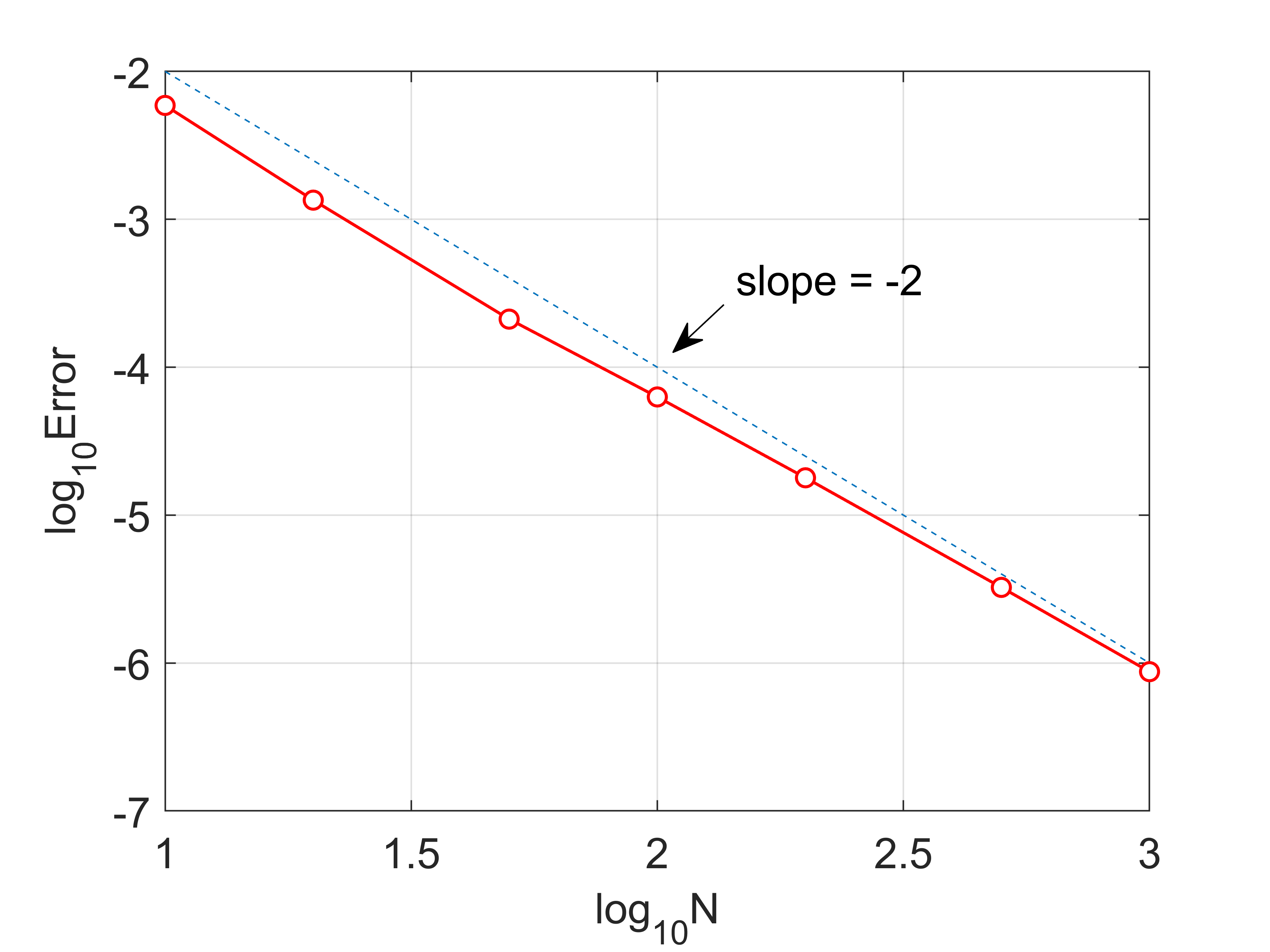
计算收敛阶
1 | % fdm1d1_error.m |
输出结果
1 | Error = |
两点边值问题(变系数)
考虑二阶常微分方程边值问题(变系数):
假定
首先取
将区间 $I=[a,b]$ 分成 $N$ 个小区间:
记
取相邻节点
又构成 $[a,b]$ 的一个剖分,称为对偶剖分。
差分方程:
当网格均匀,即
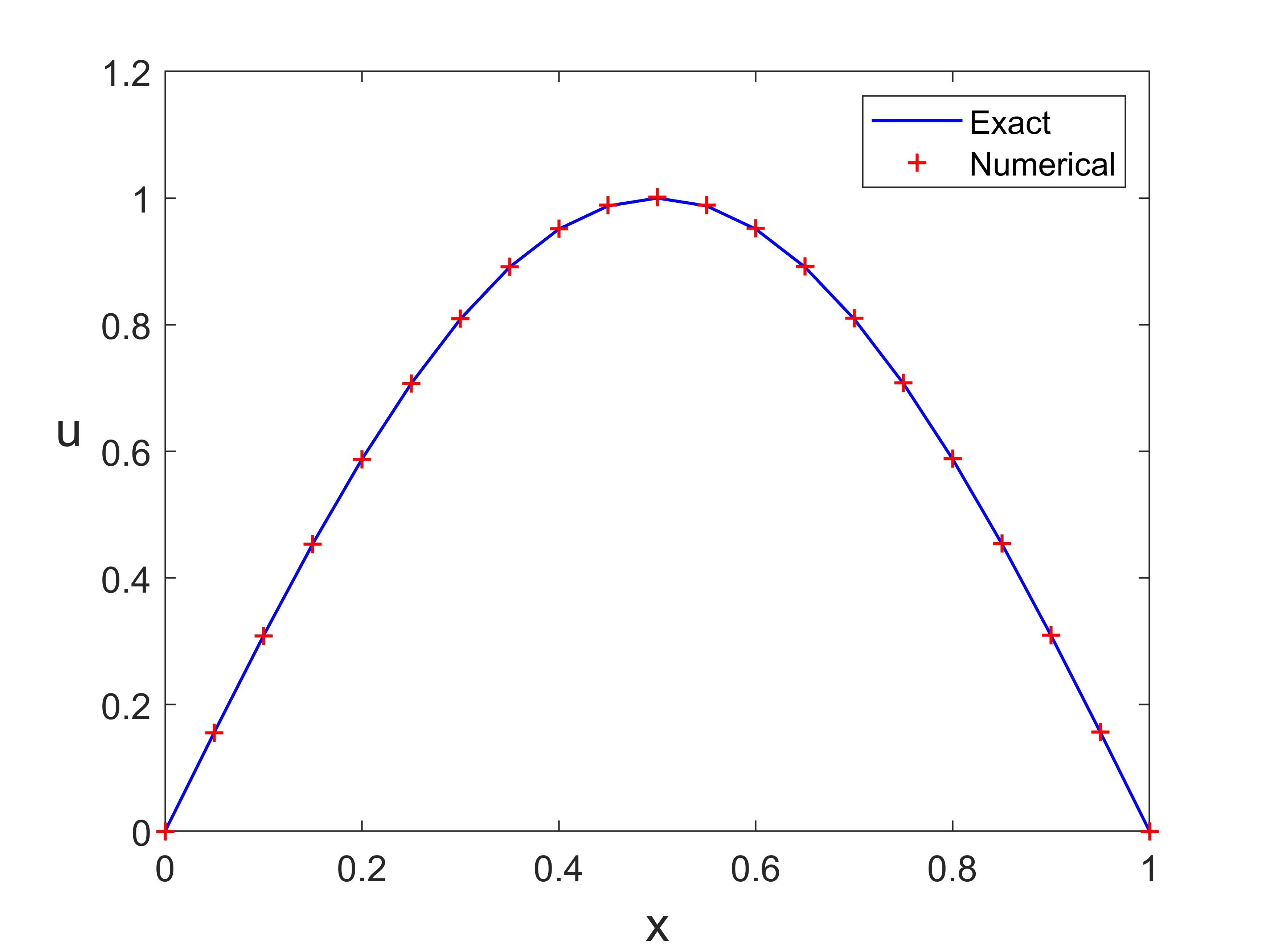
数值例子
方程的真解:
计算数值解
1 | % fdm1d2.m |
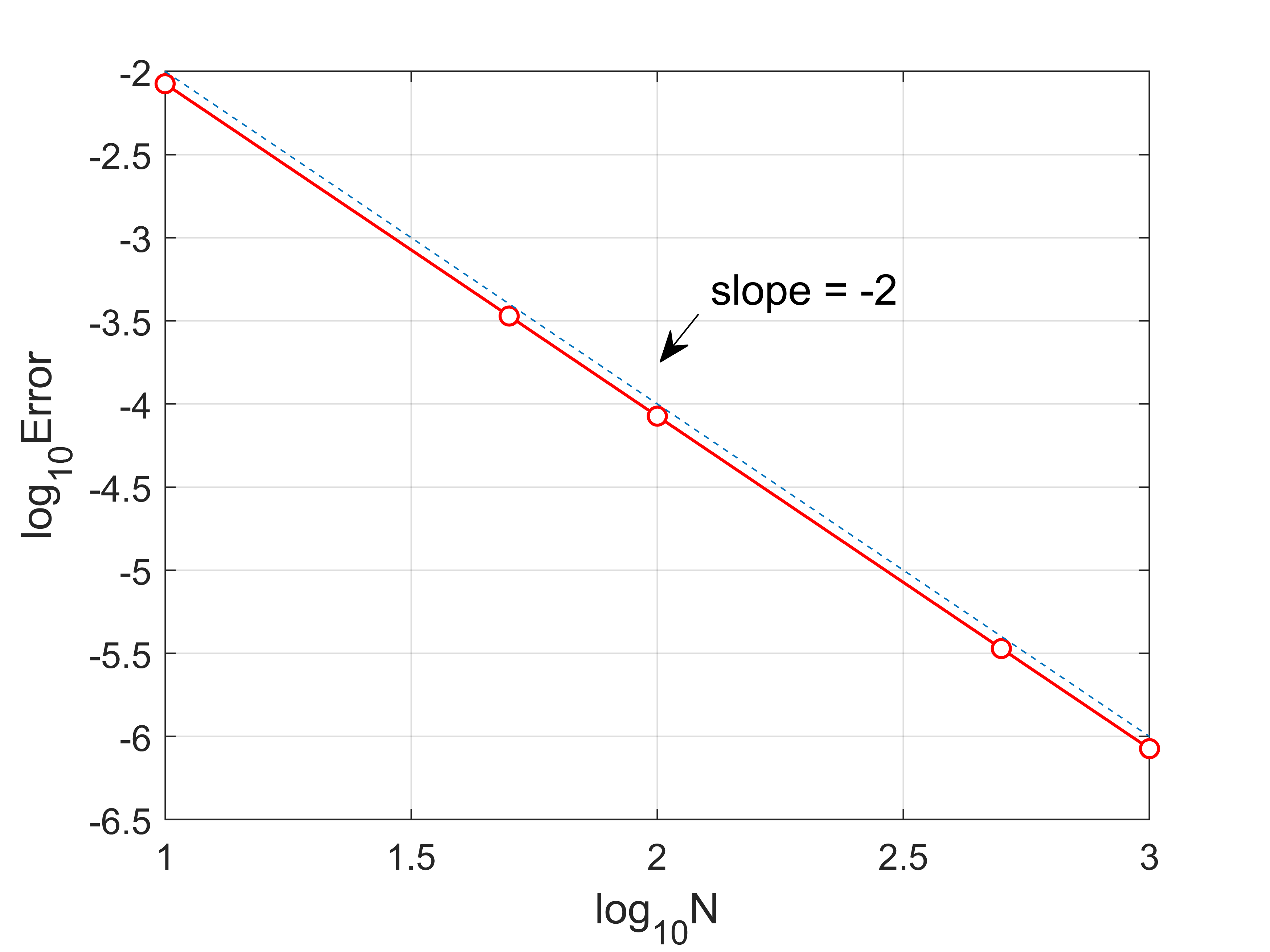
计算收敛阶1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44% fdm1d2_error.m
% finite difference method for 1D problem
% -(xu')'+x*u'=pi^2*x*sin(pi*x)-pi*cos(pi*x)+pi*x*cos(pi*x) in [0,1]
% u(0)=0, u(1)=0 ;
% exact solution : u=sin(pi*x)
clear all; close all;
Nvec=[10 20 50 100 200 500 1000]; % Number of partitions
Error=[];
for k=1:length(Nvec)
N=Nvec(k);
h=1/N;
x=0:h:1;
N=length(x)-1;
A=diag(2*x(2:N)./h^2)+diag(x(2:N-1)./(2*h)-(x(2:N-1)+0.5*h)./h^2,1)...
+diag(-x(3:N)./(2*h)-(x(3:N)-0.5*h)./h^2,-1);
b=pi^2*x(2:N).*sin(pi*x(2:N))+pi*(x(2:N)-1).*cos(pi*x(2:N));
u=A\b';
u=[0;u;0];
ue=sin(pi*x');
error=max(abs(u-ue));
Error=[Error,error];
end
plot(log10(Nvec),log10(Error),'ro-','MarkerFaceColor','w','LineWidth',1)
hold on
plot(log10(Nvec), log10(Nvec.^(-2)), '--')
grid on
%title('Convergence of Finite Difference Method','fontsize',14)
set(gca,'fontsize',14)
xlabel('log_{10}N','fontsize', 14), ylabel('log_{10}Error','fontsize',14),
% add annotation of slope
ax = [0.57 0.53];
ay = [0.68 0.63];
annotation('textarrow',ax,ay,'String','slope = -2 ','fontsize',14)
% computating convergence order
for i=1:length(Nvec)-1
order(i)=-log(Error(i)/Error(i+1))/(log(Nvec(i)/Nvec(i+1)));
end
Error
order
% print -dpng -r600 fdm1d2_error.png
% print -depsc2 fdm1d2_error.eps
输出结果
1 | Error = |