1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
clear all; close all;
Nvec=[10 50 100 500 1000];
Error=[];
fun=@(x,u) x.^2+x-u;
for k=1:length(Nvec)
N=Nvec(k);
h=1/N;
x=0:h:1;
u(1)=0;
for n=1:N
k1=fun(x(n),u(n));
k2=fun(x(n+1),u(n)+h*k1);
u(n+1)=u(n)+(h/2)*(k1+k2);
end
ue=-exp(-x)+x.^2-x+1;
error=max(abs(u-ue));
Error=[Error,error];
end
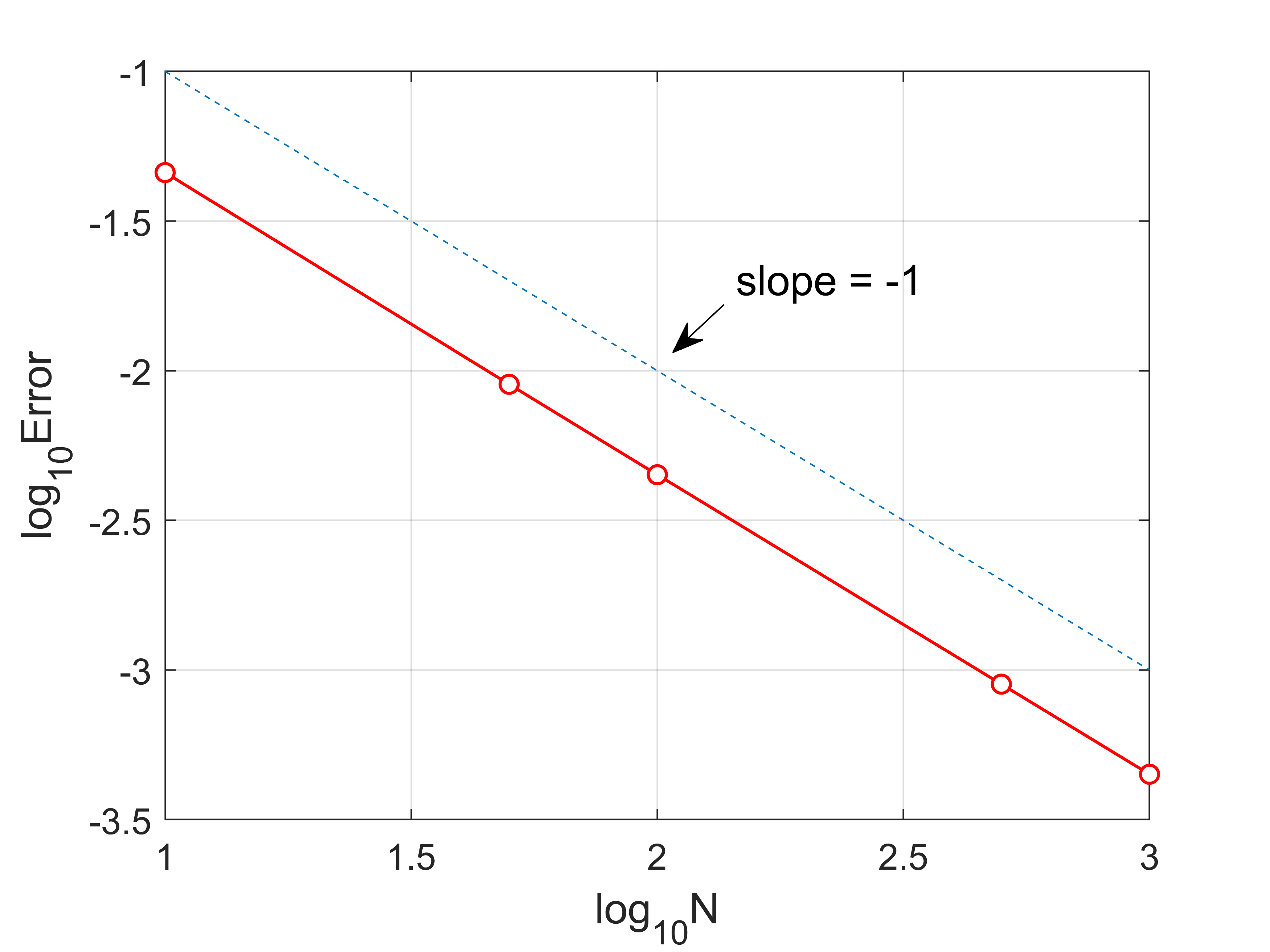
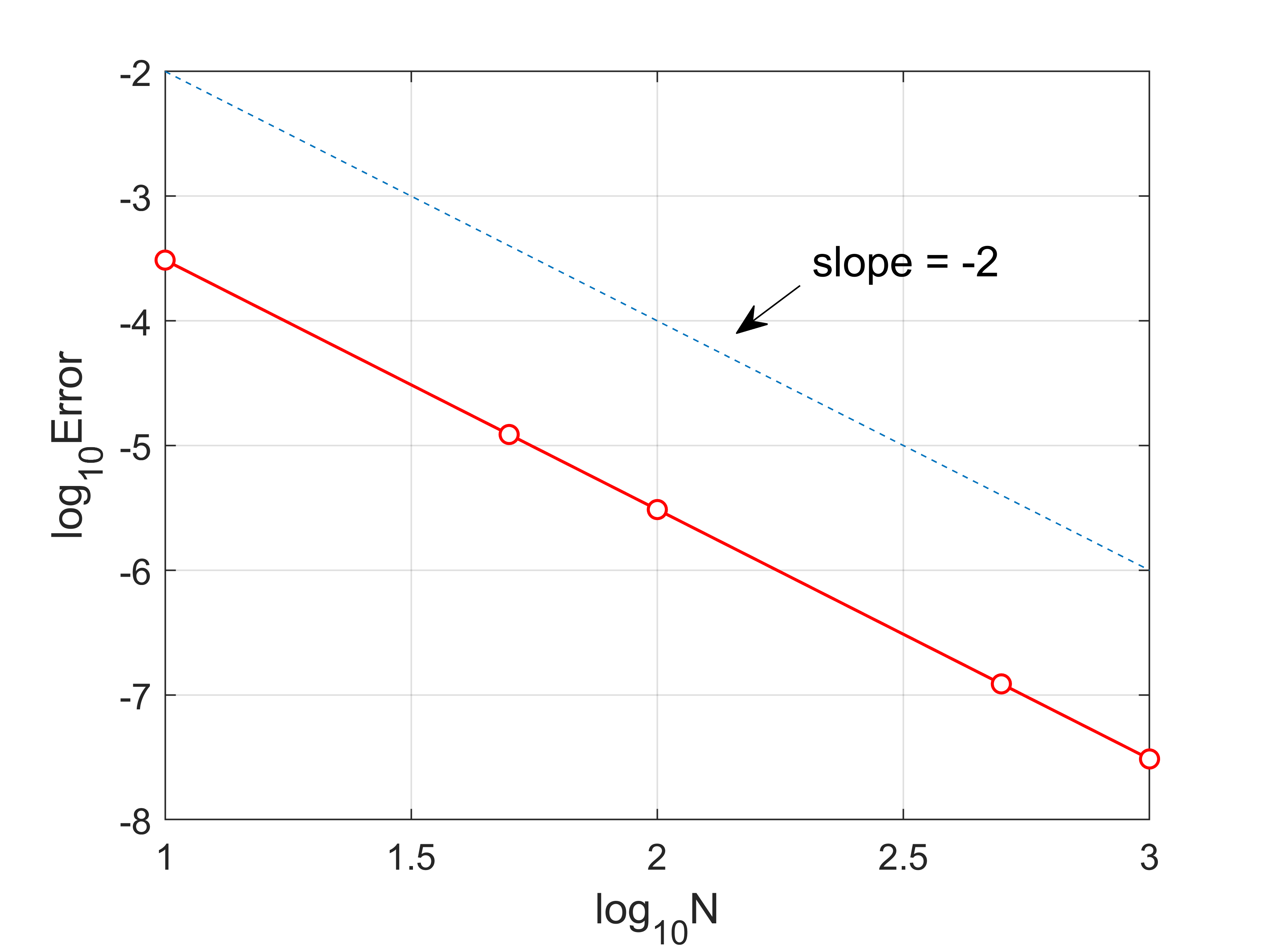
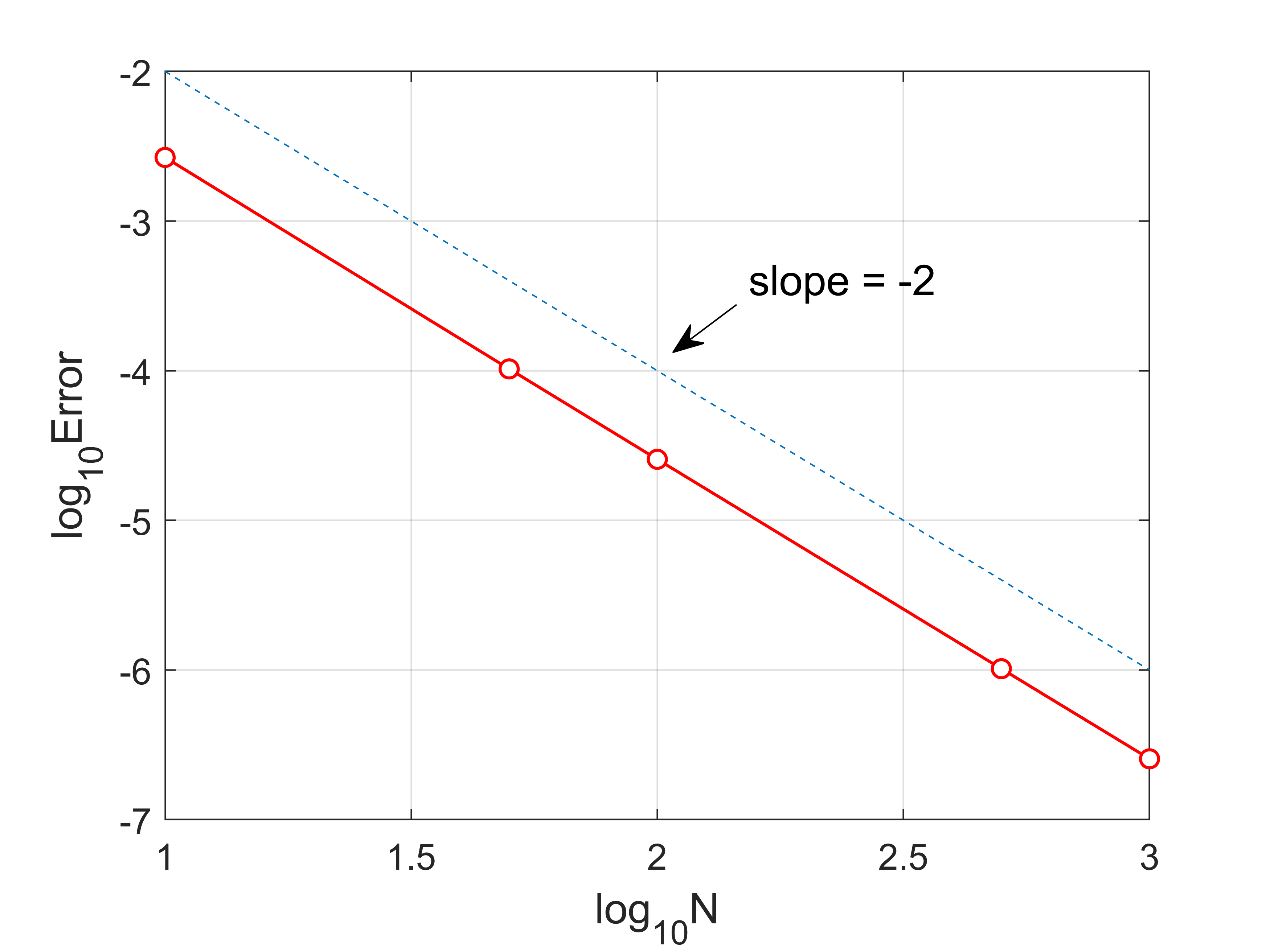
plot(log10(Nvec),log10(Error),'ro-','MarkerFaceColor','w','LineWidth',1)
hold on
plot(log10(Nvec),log10(Nvec.^(-2)),'--')
grid on
set(gca,'fontsize',12)
xlabel('log_{10}N','fontsize',14), ylabel('log_{10}Error','fontsize',14)
ax = [0.58 0.53];
ay = [0.68 0.63];
annotation('textarrow',ax,ay,'String','slope = -2 ','fontsize',14)
for n=1:length(Nvec)-1
order(n)=-log(Error(n)/Error(n+1))/(log(Nvec(n)/Nvec(n+1)));
end
Error
order
|