SMM02 半离散 Fourier 变换

本文是书籍 Spectral Method in MATLAB 第二章 Unbounded Grids: the Semidiscrete Fourier Transform 无界网格：半离散 Fourier 变换 笔记。

我们现在导出第一个谱方法，就是第一章的两边无限的矩阵。这种方法适用于离散的、无界的区域，因此不是一种实用的方法。但是，它确实介绍了推导和分析实用方法所需的数学思想。

半离散 Fourier 变换

无限网格用 $h \mathbb{Z}$表示，节点 $x_j=jh$，其中 $j \in \mathbb{Z}$ ，$\mathbb{Z}$ 是所有整数的集合。

根据半离散傅里叶变换和有限带宽 $sinc$ 函数插值的基本思想去推导 (1.4) 两边无限的矩阵。函数 $u(x)$ ($x \in \mathbb{R}$) 的 Fourier 变换后的函数 $\hat{u}(k)$ 定义为

$$\hat{u}(k)=\int_{-\infty}^{\infty} u(x) e^{-i k x} dx, \quad \color{red}{k \in \mathbb{R}}.$$

$\hat{u}(k)$ 可以解释为 $u$ 在波数 $k$ 时的振幅，将一个函数分解为其组成波的过程称为 Fourier 分析。相反地，我们可以从 $\hat{u}$ 通过 逆 Fourier 变换重构 $u$：

$$u(x)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} \hat{u}(k) e^{i kx} d k, \quad \color{red}{x \in \mathbb{R}}.$$

这是傅里叶合成。变量 $x$ 是物理变量，$k$ 是 Fourier 变量或波数。

现在考虑 $x$ 在 $h\mathbb{Z}$ 上的值而不是 $\mathbb{R}$。在这种情况下， Fourier 变换及其逆的精确变换是存在的。关键点在于，由于空间域是离散的，波数 $k$ 将不覆盖R的所有范围。相反，波数域是长度为 $2\pi/h$ 的有界区间，一个适当的选择是 $[-\pi/h,\pi/h]$。记住 $k$ 是有界的，因为 $x$ 是离散的：

产生这些联系的原因是一种称为混叠的现象。当 $k_1 \neq k_2$，两个复指数函数 $f(x)=\exp (i k_{1} x)$ 与 $g(x)=\exp (i k_{2} x)$ 在 $\mathbb{R}$ 上是不相等的。如果我们限制 $f$ 和 $g$ 到 $h\mathbb{Z}$，取 $f_j = \exp (i k_{1} x_{j})$ 和 $g_{j}=\exp (i k_{2} x_{j})$，如果 $k_1-k_2$ 是 $2\pi/h$的整数倍，对每一个 $j$ 有 $f_{j}=g_{j}$。因此，对于任何复指数 $\exp (ikx)$ 在网格 $h\mathbb{Z}$ 上有无限多的其他复指数（$k$ 的“混叠” ）与之匹配。因此，在 $2\pi/h$ 长度的间隔内计算网格的波数就足够了，并且出于对称性的原因，我们选择了间隔 $[-\pi/h,\pi/h]$。

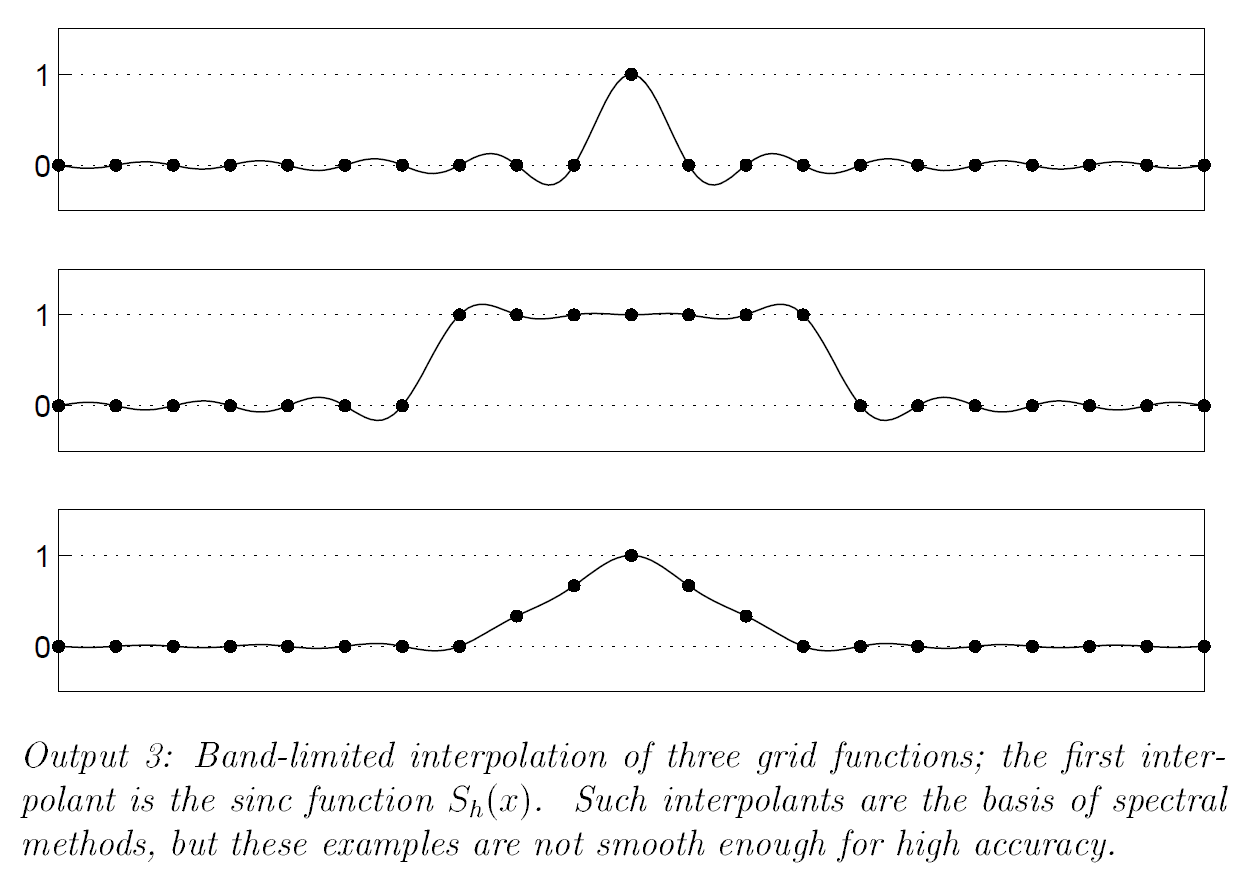
下图说明了函数 $\sin(\pi x)$ 和 $\sin(9\pi x)$ 相互“混叠”。网格节点的表示限制到了 $\frac{1}{4} \mathbb{Z}$，其中这两个函数是相同的。

“混叠”也出现在非数学生活中，例如西方电影中的“马车轮效应”。如果说照相机的快门每秒发出 24 次咔哒声，货车车轮上的辐条每秒通过垂直方向 20 次，然后车轮看起来好像以每秒 -4 辐条的速度旋转，即向后旋转。同一现象的更高频率“混叠”是频闪显微镜科学的基础，而空间而非时间的混叠会导致云纹。

对于函数 $v$ 定义在 $h\mathbb{Z}$ 上节点 $x_j$ 值为 $v_j$，半离散 Fourier 变换的定义如下

$$\hat{v}(k)=h \sum_{j=-\infty}^{\infty} e^{-i k x_{j}} v_{j}, \quad \color{red}{k \in[-\pi / h, \pi / h]}.$$

半离散 Fourier 逆变换为

$$v_{j}=\frac{1}{2 \pi} \int_{-\pi / h}^{\pi / h} e^{i k x_{j}} \hat{v}(k) dk, \quad \color{red}{j \in \mathbb{Z}}.$$

半离散 Fourier 变换 (2.3) 通过梯形公式逼近 Fourier 变换 (2.1)，半离散 Fourier 逆变换 (2.4)逼近 (2.2) 则是通过截断 $\mathbb{R}$ 到 $[-\pi /h, \pi /h]$。当 $h \rightarrow 0$，两对公式收敛。

如果“半离散 Fourier 变换”这个表达式不熟悉，那可能是因为我们给一个旧概念取了一个新名字。Fourier 级数表示有界区间上的函数，它是离散波数上复指数的和，如 (2.3)。我们用半离散 Fourier 变换来强调我们在这里关心的是逆问题：空间变量是离散的，Fourier 变量是连续的，属于有界区间 。从数学上讲，这与 Fourier 级数理论没有区别，Fourier 级数在许多书中都有介绍，是数学中应用最广泛的分支之一。

对于谱微分，我们需要一个插值函数，而反变换 上式 (2.4) 将给出一个插值函数。我们所要做的只是计算 $x \in \mathbb{R}$ 的相同公式，而不仅仅是 $x_j \in h\mathbb{Z}$。也就是说，在确定 $\hat{v}$ 之后，我们定义插值函数 $p$

$$p(x)=\frac{1}{2 \pi} \int_{-\pi / h}^{\pi / h} e^{i k x} \hat{v}(k) d k, \quad x \in \mathbb{R}$$

这是一个关于 $x$ 的解析函数，并且对每个 $j$ 都有 $p(x_j)=v_j$。而且通过推导，Fourier 变换 $\hat{p}$ 通过 (2.1) 定义为

$$\hat{p}(k)=\left\{\begin{aligned} &\hat{v}(k) && k \in[-\pi / h, \pi / h], \\ & 0 && \text{ otherwise}.\end{aligned}\right.$$

关于解析：函数 $f$ 在点 $z \in \mathbb{C}$ 处是解析的，如果它在 $z$ 附近的复数意义上是可微的，或者如果它的 Taylor 级数收敛到 $f$。

因此，p在 $[-\pi /h,\pi/h]$ 具有紧支集。我们说 $p$ 是 $v$ 的带限插值，这并不意味着 $\hat{p}$ 有紧支集，但该支集包含在特定区间 $[-\pi/h，\pi/h]$ 中。虽然对于任何网格函数都有一定数量的可能插值，但在这个意义上只有一个带限插值。这个结果被称为抽样定理，与Whittaker、Shannon 和 Nyquist 的名字有关。

我们准备给出在 $h\mathbb{Z}$ 上定义的函数 $v$ 的谱微分的前两个描述。下面是一个

• 给定 $v$，通过 (2.5) 确定其带限插值 $p$，
• 设 $w_{j}=p^{\prime}(x_{j})$.

另一个在 Fourier 空间中同样可以得到。如果可微函 $u$ 有 Fourier 变换 $\hat{u}$，则 $u’$ 的 Fourier 变换是 $ik\hat{u}(k)$：

$$\widehat{u^{\prime}}(k)=i k \hat{u}(k).$$

这个结果可以通过对 (2.2) 或 (2.5) 关于 $x$ 微分得到，因此我们有一个等价的谱微分过程：

• 给定 $v$，通过 (2.3) 计算其半离散 Fourier 变换.
• 定义 $\widehat{w}(k)=i k \hat{v}(k)$.
• 利用 $\hat{w}$ 通过 (2.4) 计算 $w$.

这两种谱微分的描述在数学上都是完整的，但是我们还没有导出矩阵 (1.4) 的系数，为此，我们可以使用傅里叶变换回代并对带限插值 $p(x)$ 有更全面的了解。令 $\delta$ 为克罗内克（Kronecker delta）函数，

$$\delta_{j}=\left\{\begin{aligned} &1 && j=0, \\ &0 && j \neq 0. \end{aligned}\right.$$

通过 (2.3)，$\delta$ 的半离散 Fourier 变换是一个常数：$\hat{\delta}(k)=h$ 对于所有的 $k \in[-\pi / h, \pi / h]$。通过 (2.5)，$\delta$ 的带限插值是

$$p(x)=\frac{h}{2 \pi} \int_{-\pi / h}^{\pi / h} e^{i k x} d k=\frac{\sin (\pi x / h)}{\pi x / h}.$$

（$x=0$ 处的值为 1）。这个著名又漂亮的函数称为 $sinc$ 函数，

$$S_{h}(x)=\frac{\sin (\pi x / h)}{\pi x / h}.$$

Sir Edmund Whittaker 称 $S_1$ “···尊贵血统在整个家族中的一种函数，其独特的属性使其与资产阶级的兄弟分离。

既然我们知道如何插值 $\delta$ 函数，我们可以插值任何函数。对于任意 $m$，带限插值是一个平移不变的过程，$\delta_{j-m}$ 的带限插值是 $S_{h}(x-x_{m})$。一般网格函数 $v$ 可以写成

$$v_{j}=\sum_{m=-\infty}^{\infty} v_{m} \delta_{j-m}$$

因此，根据半离散 Fourier 变换的线性性质，$v$ 的带限插值是转换 $sinc$ 函数的线性组合：

$$p(x)=\sum_{m=-\infty}^{\infty} v_{m} S_{h}(x-x_{m}).$$

相应的导数

$$w_{j}=p^{\prime}(x_{j})=\sum_{m=-\infty}^{\infty} v_{m} S_{h}^{\prime}(x_{j}-x_{m}).$$

现在让我们导出 (1.4) 两边无限 Toeplitz 矩阵 $D$ 的元素。上式(2.11) 可以导出 (1.5) 的矩阵方程，我们可以看出向量 $S’_h(x_j)$ 是矩阵 $D$ 的列 $m=0$ ，其他列通过适当地上下移动该列而获得。公式 (1.4) 的项是由微分练习 (2.8) 决定的

$$S_{h}^{\prime}(x_{j})=\left\{\begin{aligned} &0 && j=0, \\ &\frac{(-1)^{j}}{j h} && j \neq 0. \end{aligned}\right.$$

Program 3

% p3.m - band-limited interpolation

  h = 1; xmax = 10; clf
  x = -xmax:h:xmax;                     % computational grid
  xx = -xmax-h/20:h/10:xmax+h/20;       % plotting grid
  for plt = 1:3
    subplot(4,1,plt)
    switch plt
      case 1, v = (x==0);               % delta function
      case 2, v = (abs(x)<=3);          % square wave
      case 3, v = max(0,1-abs(x)/3);    % hat function
    end
    plot(x,v,'.','markersize',14), grid on
    p = zeros(size(xx));
    for i = 1:length(x),
      p = p + v(i)*sin(pi*(xx-x(i))/h)./(pi*(xx-x(i))/h);
    end
    line(xx,p), axis([-xmax xmax -.5 1.5])
    set(gca,'xtick',[]), set(gca,'ytick',[0 1])
  end

类似的模式适用于所有的谱配置方法。谱微分矩阵的第 $m$ 列包含值 $p^{\prime}(x_{j})$，其中 $p(x)$ 是通过在 $x_m$ 的离散 $\delta$ 函数的全局插值。

Program 3 通过绘制定义在 $\mathbb{Z}$（即 $h=1$）上的三个离散函数及其带限插值。从输出结果的三个图中的第一个图可以清楚地看出，$sinc$ 函数是平滑的。第二个图描绘了离散方波的插值，显示了 $sinc$ 插值对于逼近非光滑函数不是特别好。当 $h \rightarrow 0$ 时，不连续处附近的振荡幅度不会减小，甚至在空间上也没有很好的局部化。这种在间断附近产生的振荡称为吉布斯现象。第三幅图显示了离散三角波或“hat函数”及其插值。这里的插值比较好，但仍然不令人印象深刻。实际上，正如我们将在第4章中详细解释的那样，插值的精度取决于 $u$ 的光滑性，并且这些例子不是很平滑。每一个 $u$ 的导数都提高了 1 阶精度。

为了找到高阶谱导数，我们可以多次对 $p(x)$ 微分。例如

$$S_{h}^{\prime \prime}\left(x_{j}\right)=\left\{\begin{array}{ll}-\frac{\pi^{2}}{3 h^{2}} & j=0, \\ 2 \frac{(-1)^{j+1}}{j^{2} h^{2}} & j \neq 0.\end{array}\right.$$

结果告诉我们对称双无穷 Toeplitz 矩阵 $D$ 的每一列的项对应的二阶导数是

$$D^{2} v=\frac{2}{h^{2}} \left(\begin{array}{cccc} & \ddots & & \vdots & & & \\ & \ddots & & -\frac{1}{4} & & & \\ & \ddots & & 1 & & & \\ & & & -\frac{\pi^{2}}{6} & & & \\ & & & 1 & & \ddots & \\ & & & -\frac{1}{4} & & \ddots & \\ & & & \vdots & & \ddots & \end{array}\right) v.$$

本章小结

在 $h\mathbb{Z}$ 网格上的函数 $v$ 有一个唯一的插值 $p$，它的频带仅限于 $[-\pi/h,\pi/h]$ 区间内的波数。我们可以通过计算 $ik\hat{v}$ 的半离散 Fourier 逆变换来计算网格上的 $p$，或者作为 $sinc$ 函数平移的导数的线性组合。