SMM01 微分矩阵

本文是书籍 Spectral Method in MATLAB 第一章 Differentiation matrices 微分矩阵 笔记。

从一个基本问题出发。 给定一组网格节点 和相应的函数值 ，如何使这些数据逼近 的导数？可能立即想到的方法是某种有限差分公式。 我们将从有限差分方法开始去学习谱方法。

二阶差分

考虑等距剖分 , 对于每一个 有 ，这组点对应的函数值 ：

令 表示 的逼近， 表示 的导数在 处的值。 标准二阶有限差分格式

$$w_{j}=\frac{u_{j+1}-u_{j-1}}{2 h}.$$

可以通过 与 的泰勒展开得到。
为了简单起见，假设问题是周期性的，取 和 。然后我们可以把离散微分过程表示为矩阵向量乘积

$$\left(\begin{array}{c}w_{1} \\ \\ \vdots \\ \\ w_{N}\end{array}\right)=h^{-1} \left(\begin{array}{ccccc}0 & \frac{1}{2} & & & -\frac{1}{2} \\ -\frac{1}{2} & 0 & \ddots & & \\ & & \ddots & & \\ & & \ddots & 0 & \frac{1}{2} \\ \frac{1}{2} & & & -\frac{1}{2} & 0\end{array}\right) \left(\begin{array}{c}u_{1} \\ \\ \vdots \\ \\ u_{N}\end{array}\right)$$

稀疏矩阵中的省略项为零。观察这个矩阵可知是 Toeplitz 矩阵，沿着对角线有相同的数，比如元素 的值只与 有关。 实际上，它也是循环的，这意味着 仅依赖于 。 这个矩阵对角线 “环绕” 的。

另一种推导以上两个方程的方法是通过以下的局部插值和微分过程:

对于 ，

• 令 是不大于 2 次的多项式，, , 与 .
• 设 .

可以很容易地看出，对于固定的插值函数

$$p_{j}(x)=u_{j-1} a_{-1}(x)+u_{j} a_{0}(x)+u_{j+1} a_{1}(x),$$

其中

• ，
• ，
• .

在 时求微分并求值可以得到上式 。

四阶差分

这种局部插值的推导表明能够推广到更高阶。下面是四阶差分格式推导：

对于 ，

• 令 是不大于 4 次的多项式，, , 与 .
• 设 .

假设数据是周期的，可知方程组等价于矩阵向量乘积

$$\left(\begin{array}{c}w_{1} \\ \\ \\ \vdots \\ \\ \\ w_{N}\end{array}\right)=h^{-1} \left(\begin{array}{ccccccc} & & \ddots & & & &{\frac{1}{12}}&{-\frac{2}{3}}\\ & & \ddots & -\frac{1}{12} & & & &{\frac{1}{12}}\\ & & \ddots &{\frac{2}{3}}& \ddots & & \\ & & \ddots & 0 & \ddots & & \\ & & \ddots &{-\frac{2}{3}}& \ddots & & \\ -\frac{1}{12} & & & \frac{1}{12} & \ddots & & \\ {\frac{2}{3}}&{-\frac{1}{12}}& & & \ddots & \end{array}\right) \left(\begin{array}{c}u_{1} \\ \\ \\ \vdots \\ \\ \\ u_{N}\end{array}\right)$$

这是一个五对角而不是三对角的循环矩阵。

以上两个矩阵的矩阵是微分矩阵的例子，它们的精度分别为2阶和4阶。对一个足够光滑的函数 进行采样获得的 ，相应的离散逼近的收敛速率分别为 与 ，通过泰勒展开可以验证这一点。

Program 1

第一个 MATLAB 程序，Program 1，演示了四阶差分方法的例子，选取 在 上的周期数据。

该程序对不同 时差分逼近 与精确导数 进行了比较。 因为使用了 MATLAB 稀疏矩阵 sparse ，这个代码在电脑上运行几分之一秒就运行出来了，即使它矩阵维数大到 4096。 四阶精度是明显的。 这是我们第一个也是最后一个没有使用谱方法的例子。

% p1.m - convergence of fourth-order finite differences

% For various N, set up grid in [-pi,pi] and function u(x):
  Nvec = 2.^(3:12);
  clf, subplot('position',[.1 .4 .8 .5])
  for N = Nvec
    h = 2*pi/N; x = -pi + (1:N)'*h;
    u = exp(sin(x)); uprime = cos(x).*u;

    % Construct sparse fourth-order differentiation matrix:
    e = ones(N,1);
    D =   sparse(1:N,[2:N 1],2*e/3,N,N)...
        - sparse(1:N,[3:N 1 2],e/12,N,N);
    D = (D-D')/h;

    % Plot max(abs(D*u-uprime)):
    error = norm(D*u-uprime,inf);
    loglog(N,error,'.','markersize',15), hold on
  end
  grid on, xlabel N, ylabel error
  title('Convergence of fourth-order finite differences')
  semilogy(Nvec,Nvec.^(-4),'--') 
  text(105,5e-8,'N^{-4}','fontsize',18)

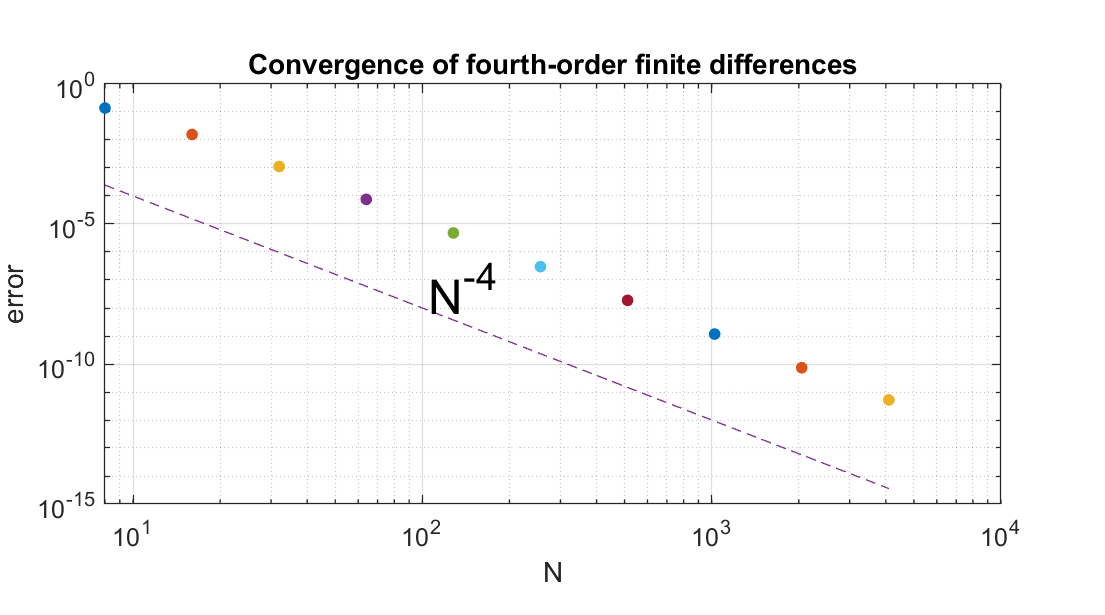
我们研究了二阶和四阶有限差分。很明显，考虑六阶、八阶和更高阶的方法将导致带宽增加的循环矩阵。谱方法背后的思想是，将这一过程带到极限，并使用无穷阶和无限带宽的微分公式——比如一个稠密矩阵。在下一章中，我们将证明在这个极限下，对于一个无限等距网格，我们得到以下无限矩阵

$$D=h^{-1} \left(\begin{array}{ccccccc} & & & & \vdots & & & & & \\ & & \ddots & & \frac{1}{3} & & & & \\ & & \ddots & & -\frac{1}{2} & & & & \\ & & \ddots & & 1 & & & & \\ & & & & 0 & & & & \\ & & & & -1 & & \ddots & & \\ & & & & \frac{1}{2} & & \ddots & & \\ & & & & -\frac{1}{3} & & \ddots & & \\ & & & & \vdots & & & & \\ \end{array}\right).$$

这是一个反对称（）两边无限的 Toeplitz 矩阵，也称为 Laurent 算子。除主对角线上的项外，它的所有项都不是零。

谱配置方法

实际操作中一个矩阵不可能是无限的。对于有限网格，下面是谱配置方法

• 令 是一个单独的函数（与 无关），使得对所有的 成立 .
• 设 .

我们可以自由选择 来解决问题。 对于一个周期性的区域，自然的选择是在一个等步长的网格上的三角多项式，由此产生的 “Fourier” 方法将在第4章和后面章节中提到。 对于非周期区域，不规则网格上的代数多项式是正确的选择，我们将从第5章和第6章开始介绍这种类型的 “Chebyshev” 方法。

对于有限的 ，为了简单起见直接取 ，这是在第3章中为周期的规则网格导出 的稠密矩阵

$$D_{N}= \left(\begin{array}{ccccccc} & & & & \vdots & & & & & \\ & & \ddots & & \frac{1}{2}\cot\frac{3h}{2} & & & & \\ & & \ddots & & -\frac{1}{2}\cot\frac{2h}{2} & & & & \\ & & \ddots & & \frac{1}{2}\cot\frac{1h}{2} & & & & \\ & & & & 0 & & & & \\ & & & & -\frac{1}{2}\cot\frac{1h}{2} & & \ddots & & \\ & & & & \frac{1}{2}\cot\frac{2h}{2} & & \ddots & & \\ & & & & -\frac{1}{2}\cot\frac{3h}{2} & & \ddots & & \\ & & & & \vdots & & & & \\ \end{array}\right).$$

Program 2

% p2.m - convergence of periodic spectral method (compare p1.m)

% For various N (even), set up grid as before:
  clf, subplot('position',[.1 .4 .8 .5])
  for N = 2:2:100;
    h = 2*pi/N;
    x = -pi + (1:N)'*h;
    u = exp(sin(x)); uprime = cos(x).*u;

    % Construct spectral differentiation matrix:
    column = [0 .5*(-1).^(1:N-1).*cot((1:N-1)*h/2)];
    D = toeplitz(column,column([1 N:-1:2]));

    % Plot max(abs(D*u-uprime)):
    error = norm(D*u-uprime,inf);
    loglog(N,error,'.','markersize',15), hold on
  end
  grid on, xlabel N, ylabel error
  title('Convergence of spectral differentiation')

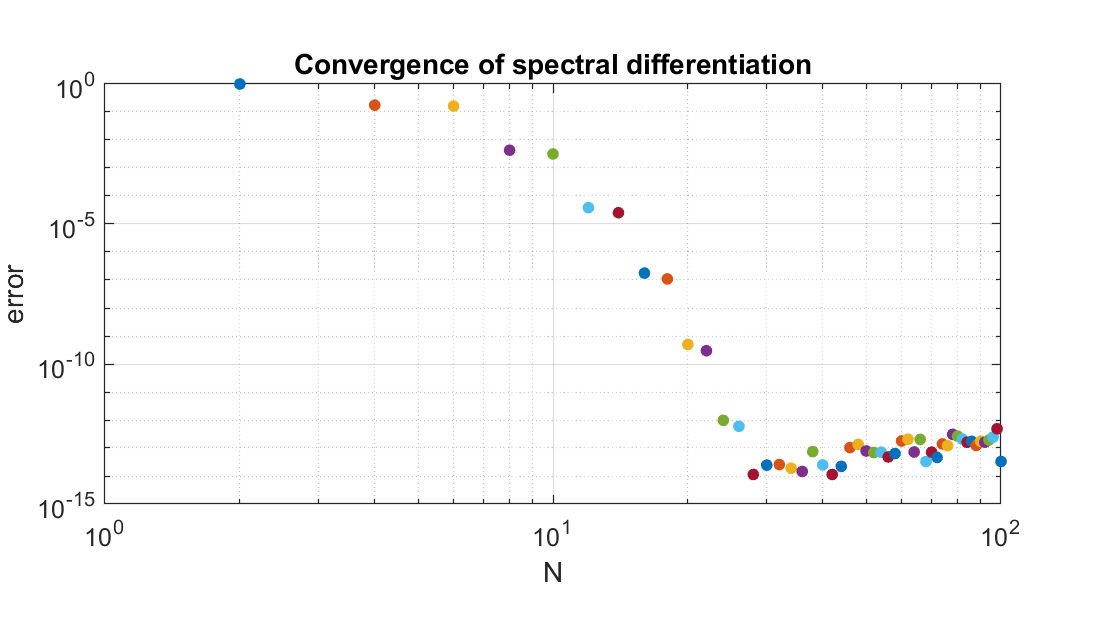
注：谱方法具有 “谱精度”，直到舍入误差超过 。这个矩阵是稠密的，但是 的值比程序1小得多。

观察余切函数，可以发现这个矩阵确实和 Toeplitz 矩阵一样是循环的。

程序2与程序1相同，只是谱方法替换了差分方法，结果有什么不同！输出2中的误差下降得非常快，直到达到如此高的精度，以至于计算机上的舍入误差阻止了进一步的改进。这种显著的行为称为谱精度。我们将在第4章中给出这个短语的更精确的描述，但是现在，需要注意的是，它与有限差分法和有限元法的收敛速度有多大的不同。随着 的增加，有限差分法或有限元法中的误差收敛速率 ，常数 取决于逼近阶数和解的光滑性。对于谱方法。如果解是无穷可微的，对于每一个 的收敛速度为 ，如果解是适当解析的，收敛速度甚至比 （）的速度更快。

我们所描述的矩阵是循环的。循环矩阵的作用是卷积，我们将在第3章中看到，卷积可以通过离散傅里叶变换来计算。从历史上看，正是1965年快速傅里叶变换（FFT）的发现，导致了人们对谱方法的兴趣在1970年代激增。第8章 FFT 不仅适用于等距网格上的三角多项式，也适用于Chebyshev网格上的代数多项式。然而，即使没有 FFT 的情况下谱方法也是很强大的。在许多应用中，使用矩阵计算的结果是非常令人满意的。

舍入误差

关于舍入误差，标准IEEE双精度格式 (Double-precision floating-point format) , 这意味着每次加法, 乘法, 除法和减法都会产生完全正确的结果乘以某个因子 with .

本章小结

谱配置法的基本原理是在网格上给定离散数据，对数据进行全局插值，然后计算插值在网格上的导数。 对于周期性问题，我们通常在等距点上使用三角插值，对于非周期性问题，我们通常在不等距点上使用多项式插值。